2021年度 作品紹介3:Vicsek Model の3Dシミュレーション (田渕辰悟)
物理科学系B3の田渕辰悟さんによる作品です。
作品概要
Vicsek modelの3Dシミュレーションです。 Vicsek modelとは鳥とか魚群で見られるような集団的な挙動の発現を、各粒子の単純な行動パターンに起因させているモデルです。 粒子の細かい挙動モデルに関してはもっぱら Lain D. Couzin (2002)を参考にしました。
個別の粒子に単純な行動パターンを与えて、鳥とか魚群のような集団的な挙動が発現するVicsek modelをunityでやったやつ、サイトにアップしました!⇒https://t.co/FmutoH9HfA pic.twitter.com/KclWomOMMs
— たぶち (@goppier23) February 6, 2022
粒子のだいたいの挙動
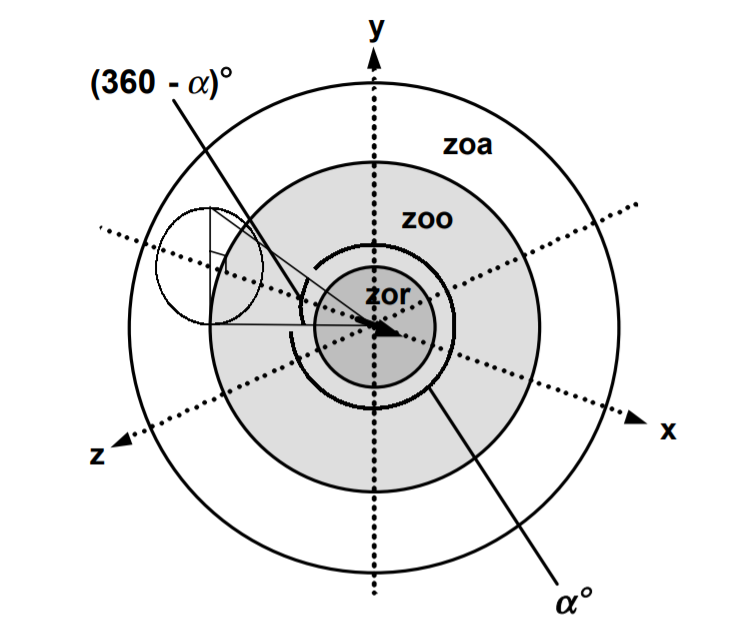
出典:Lain D. Couzin (2002) おおまかな各粒子の行動の決め方を示す模擬コード↓。
近傍にいる粒子を調べる。
視界(alpha)外の粒子は調べない。
次進む方向をVとする。
V = 今向いている方向
if(zor(zone of repulsion) に他の粒子がいる){
V = zorにいる他の粒子とできる限り遠ざかる方向
}
else{
if(zoo(zone of orientation)に粒子がいる){
if(zoa(zone of attraction)に粒子がいる){
no = zooにいる粒子の数
na = zoaにいる粒子の数
V = zooにいる粒子とできるだけ向きが揃う方向*no + zoaにいる粒子の重心にできるだけ近づける方向*na
}
else{
V = zooにいる粒子とできるだけ向きが揃う方向
}
}
else if(zoaに粒子がいる){
V = zoaにいる粒子の重心にできるだけ近づける方向
}
}
V = GaussianDistribution(mean = V, stdev = 適当な値)
0.1秒後に再び繰り返す。なぜ0.1秒なのかというと、それが金魚の反応速度だからとかなんとか。
これだけで下のような面白い集団的挙動が発現します。
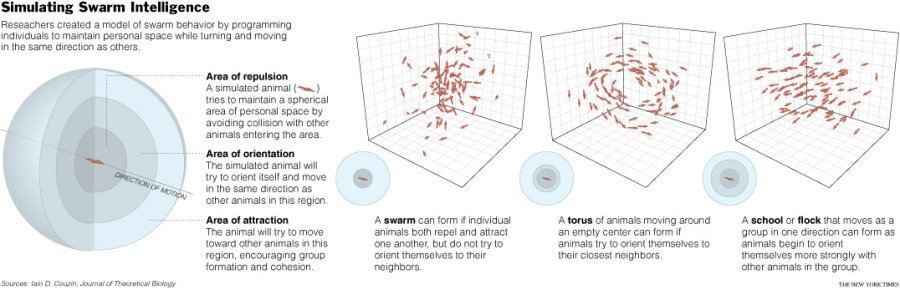 (Modeling animal behaviour より)
(Modeling animal behaviour より)
障害物のよけ方
粒子は障害物を勝手によけてくれます。
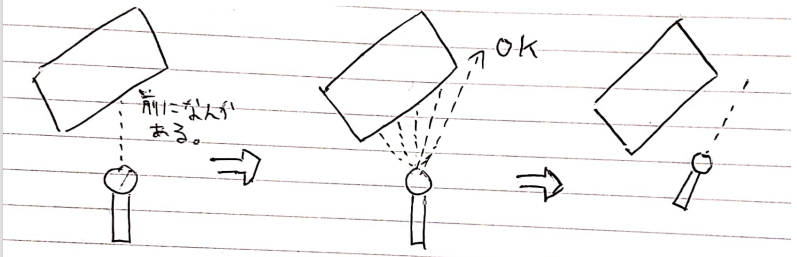 この画像で示したような二次元の場合では、障害物のない方向がみつかるまで、左右に角度を少しづつ大きくしながら探索します。
3次元でもだいたい同じようなことをします。3次元の場合は球面上をまんべんなく探索します。そこで球面上に点をまんべんなくとる方法として、ここで紹介されている”Fibonacci sphere algorithm”(フィボナッチ球アルゴリズム?)を採用しています。
この画像で示したような二次元の場合では、障害物のない方向がみつかるまで、左右に角度を少しづつ大きくしながら探索します。
3次元でもだいたい同じようなことをします。3次元の場合は球面上をまんべんなく探索します。そこで球面上に点をまんべんなくとる方法として、ここで紹介されている”Fibonacci sphere algorithm”(フィボナッチ球アルゴリズム?)を採用しています。