今回(2017年度)のスタディグループで作ってもらった作品を順に紹介していきたいと思います

最初は外村一朗さん (数理科学系4回生) の作品です. 色々な3次元の常微分方程式による力学系の軌道を描いて見ることができます.

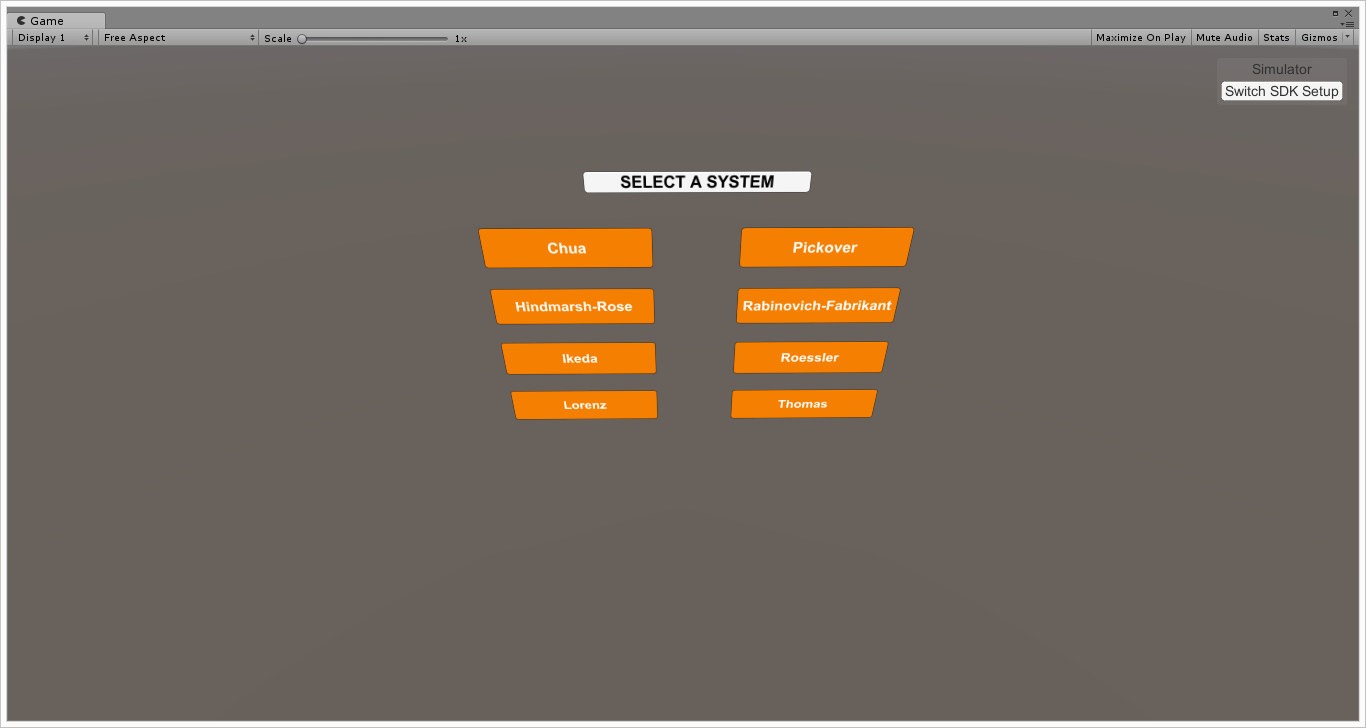
力学系の選択画面

Lorenz-63 systemのアトラクタ

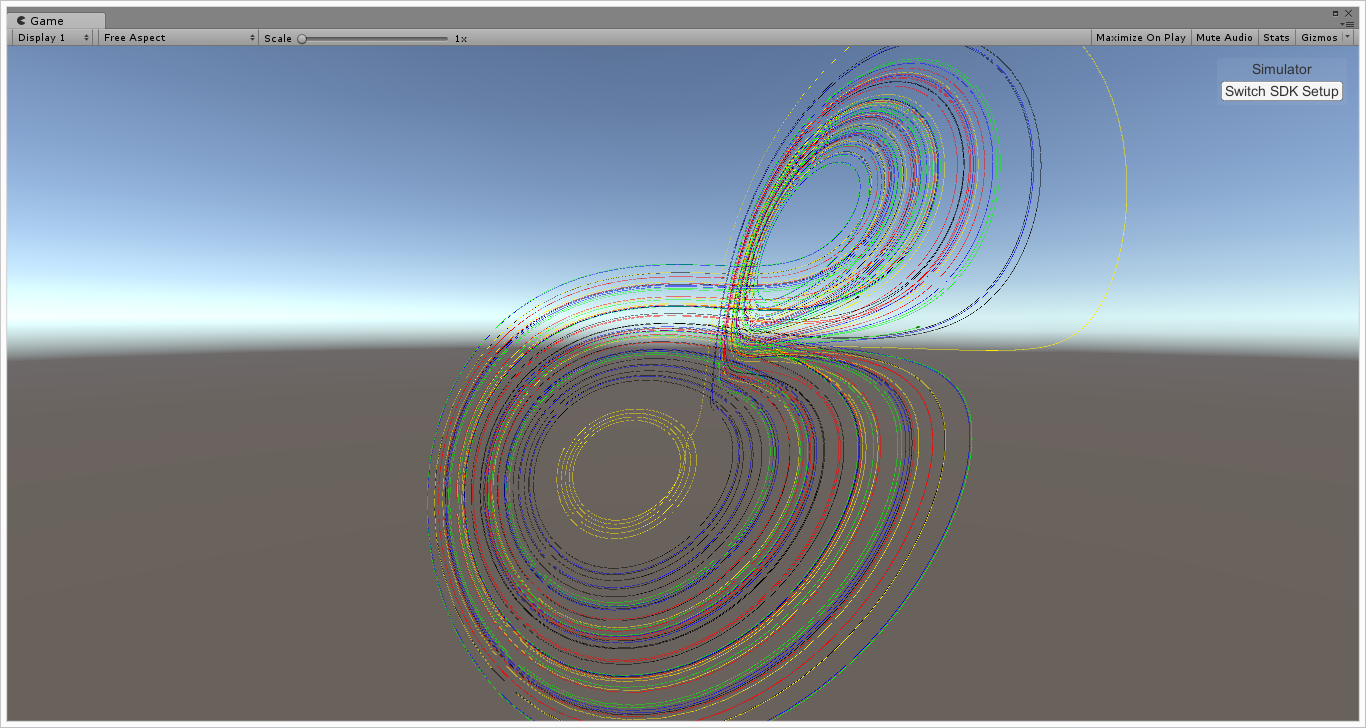
\(\left\{\begin{aligned} \frac{dx}{dt} &= s(y - x), \\ \frac{dy}{dt} &= x(r - z) - y, \\ \frac{dz}{dt} &= xy - bz. \end{aligned}\right.\) (s, r, bはパラメータ.)

Roessler systemのアトラクタ

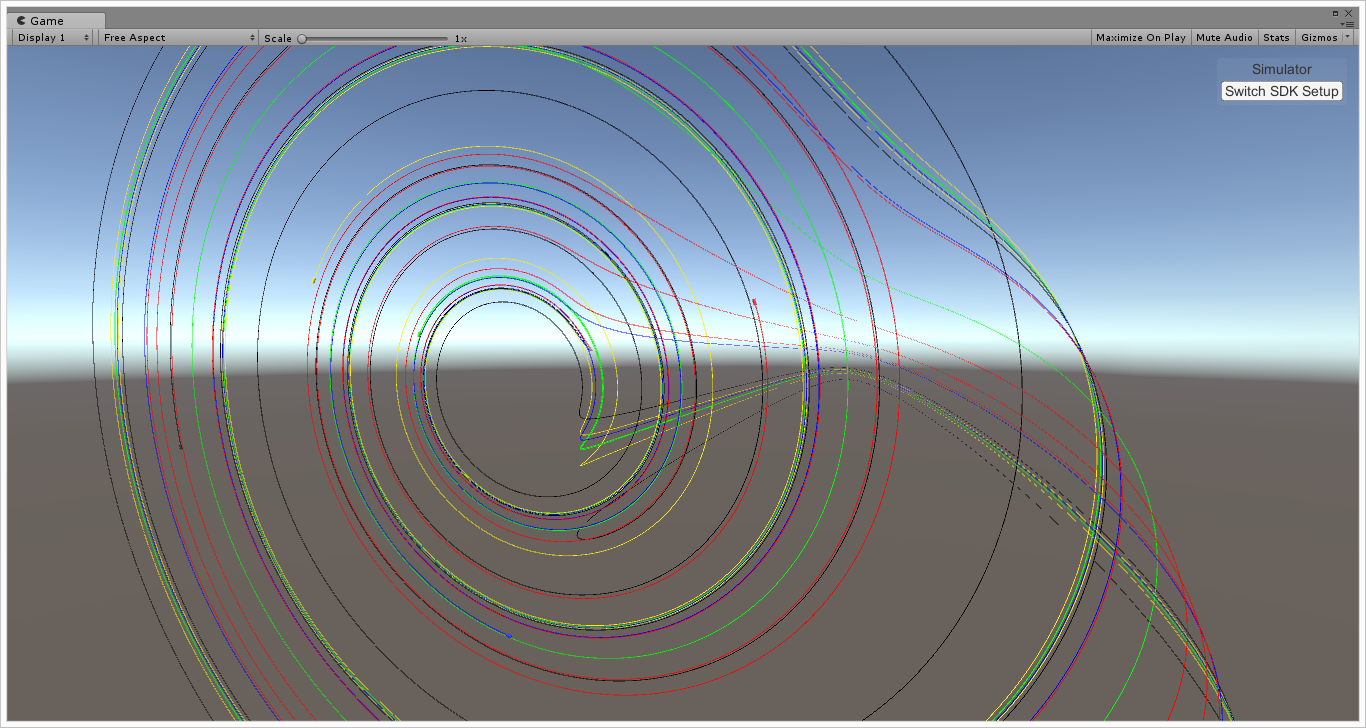
\(\left\{\begin{aligned} \frac{dx}{dt} &= -y - z, \\ \frac{dy}{dt} &= x + ay, \\ \frac{dz}{dt} &= b + z(x - c). \end{aligned}\right.\) (a, b, cはパラメータ.)

Thomas’ systemのアトラクタ

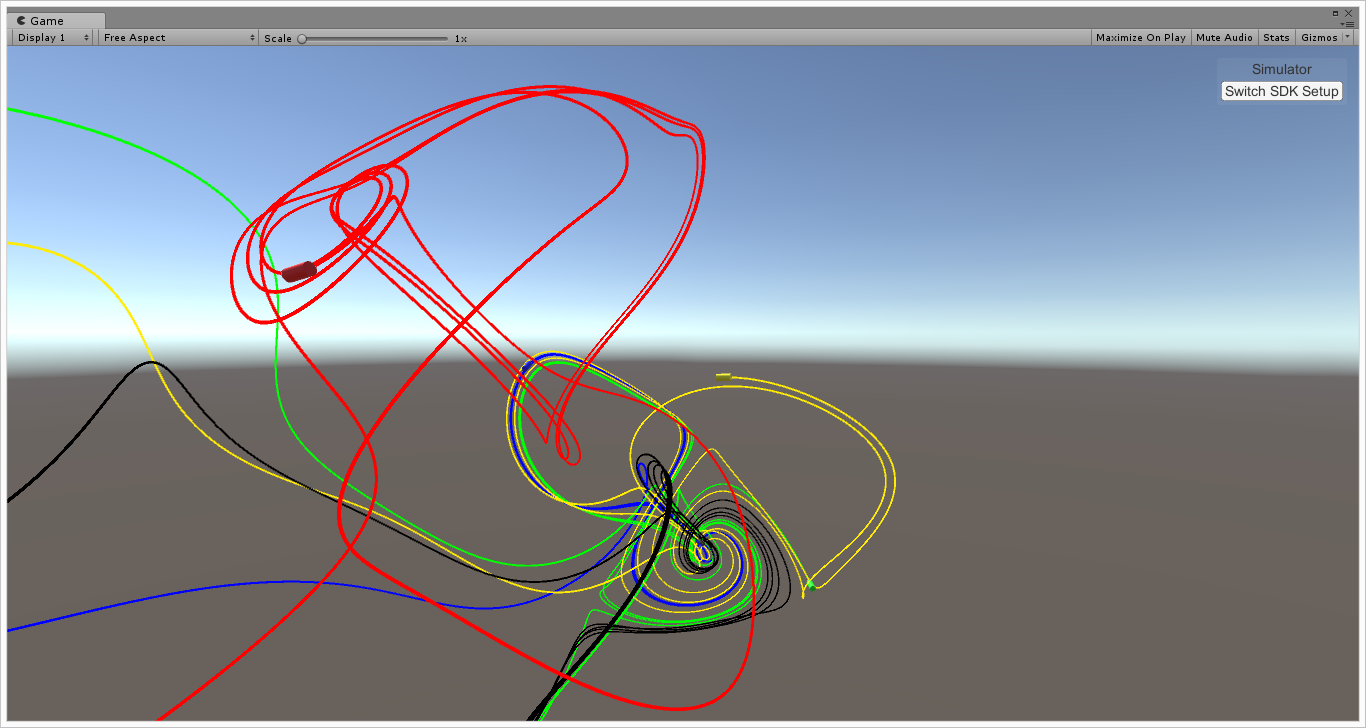
\(\left\{\begin{aligned} \frac{dx}{dt} &= \sin(y) - bx, \\ \frac{dy}{dt} &= \sin(z) - by, \\ \frac{dz}{dt} &= \sin(x) - bz. \end{aligned}\right.\) (bはパラメータ.)